Ecuación cuadrática

Esto es una ecuación cuadrática:

(a, b, y c pueden tener cualquier valor, excepto que a no puede ser 0.)

La letra "x" es la variable o incógnita, y las letras a, b y c son los coeficientes (lee las Definiciones básicas de Álgebra)

Y el nombre cuadrática viene de "cuad" que quiere decir cuadrado, porque el exponente más grande es un cuadrado (en otras palabras x²).

Ejemplos de ecuaciones cuadráticas:

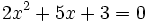En esta a=2, b=5 y c=3

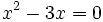Aquí hay una un poco más complicada:

¡Ups! Esta no es una ecuación cuadrática, porque le falta el x² (es decir a=0, y por eso no puede ser cuadrática)

Las ecuaciones cuadráticas se pueden resolver usando una fórmula especial llamada fórmula cuadrática:

	El "±" quiere decir que tienes que hacer más Y menos, ¡así que normalmente hay dos soluciones!

	La parte azul (b² - 4ac) se llama discriminante, porque sirve para "discriminar" (decidir) entre los tipos posibles de respuesta: si es positivo, hay DOS soluciones si es cero sólo hay UNA solución, y si es negativo hay dos soluciones que incluyen números imaginarios . Solución Para resolverla, sólo pon los valores de a,b y c en la fórmula cuadrática y haz los cálculos. Ejemplo: resuelve 5x² + 6x + 1 = 0 Fórmula cuadrática: x = [ -b ± √(b²-4ac) ] / 2a Los coeficientes son: a = 5, b = 6, c = 1 Sustituye a,b,c: x = [ -6 ± √(6²-4×5×1) ] / 2×5 Resuelve: x = [ -6 ± √(36-20) ]/10 = [ -6 ± √(16) ]/10 = ( -6 ± 4 )/10 Respuesta: x = -0.2 and -1 (Comprobación: 5×(-0.2)² + 6×(-0.2) + 1 = 5×(0.04) + 6×(-0.2) + 1 = 0.2 -1.2 + 1 = 0 5×(-1)² + 6×(-1) + 1 = 5×(1) + 6×(-1) + 1 = 5 - 6 + 1 = 0)

Algunas ecuaciones no parece que sean cuadráticas, pero con manipulaciones astutas se pueden transformar en una:

Disfrazadas	Qué hacer	En forma estándar	a, b y c
x² = 3x -1	Mueve todos los términos a la izquierda	x² - 3x + 1 = 0	a=1, b=-3, c=1
2(x² - 2x) = 5	Desarrolla paréntesis	2x² - 4x - 5 = 0	a=2, b=-4, c=-5
x(x-1) = 3	Desarrolla paréntesis	x² - x - 3 = 0	a=1, b=-1, c=-3
5 + 1/x - 1/x² = 0	Multiplica por x²	5x² + x - 1 = 0	a=5, b=1, c=-1